Multiple-head Finite Automata
Greg Bryant, 1987
Abstract:
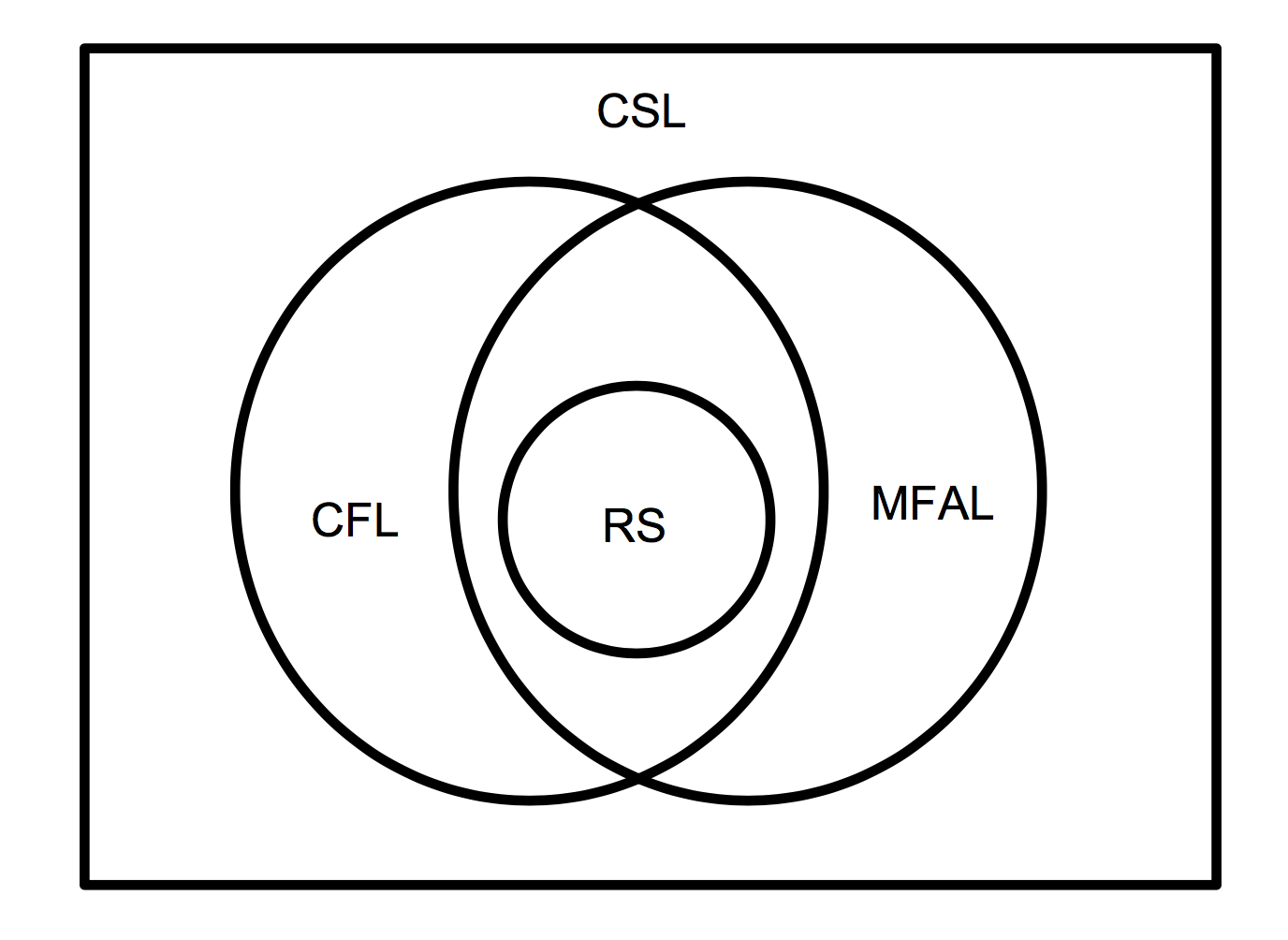
A new generalization of Finite Automata (FA) called Multiple-head Finite Automata (MFA) is described. MFA accepts a set of languages (MFAL) that do not fit the proper hierarchy of mappings between machines and language classes, often known as the Chomsky hierarchy. MFAL includes regular sets (RS), often written as regular expressions (RE). MFAL are a proper subset of context sensitive languages (CSL). But MFAL cut across context-free language (CFL) partitions: there are CFL that cannot be recognized by a MFA, and there are MFA languages that are not context-free, i.e. cannot be recognized by a standard pushdown automata. Since standard FA are considered 'Finite Machines', and pushdown automata are considered constrained 'Infinite Machines', this anomalous set implies that the distinctions between finite and infinite machines are not sufficiently well-defined.
[Note, 1988: MFAL were discovered independently in 1965. But the result never entered standard theoretical or pedagogical works. The implications here are the work of the present author.]
Keywords: automata, languages, finite automata, finite-state machines, grammars, translators, parallel processing
I. FA that accepts more than regular sets
In the finite control model of FA, the machine comes in contact with a tape, representing a string of symbols, by means of a single read head, or input.
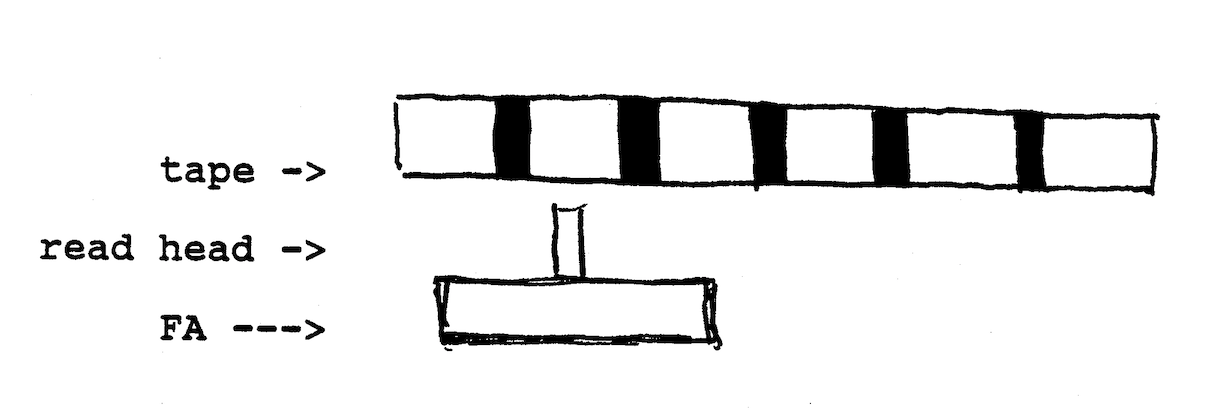
Consider instead a finite state machine with a finite number of read-only heads, all reading the same tape. This is essentially a finite number of finite control models linked together.
A two-head machine of this type can accept palindromes. A one-head FA cannot. Palindromes were previously thought to be outside the recognition ability of finite automata.
Here is how these FA machines can accept palindromes. Place one end of the tape on the leftmost head, and the other end on the rightmost head.
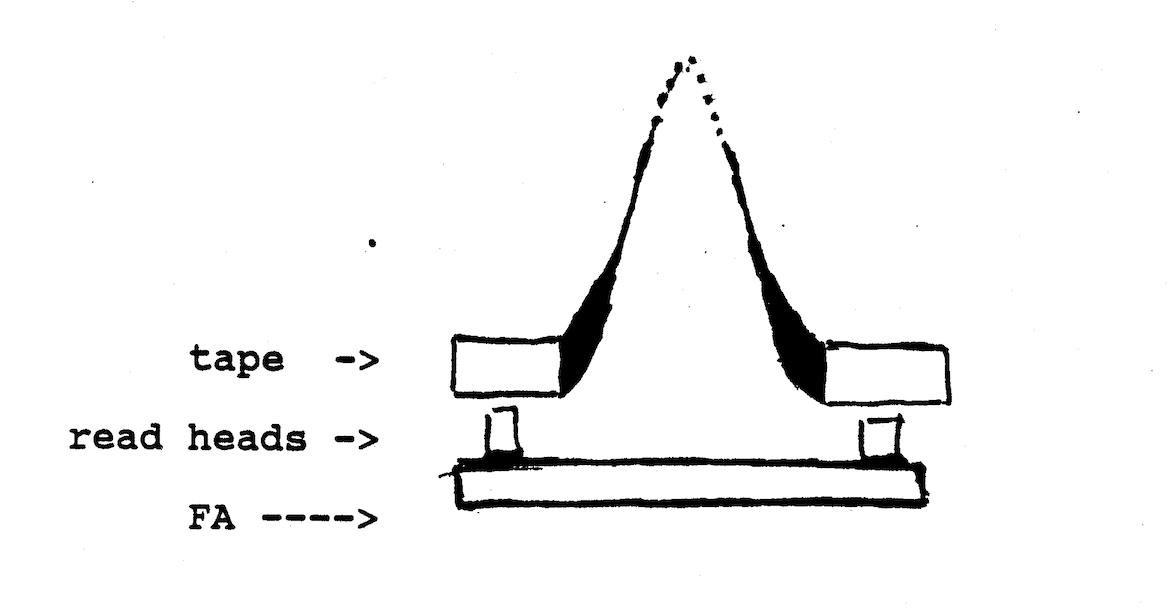
The algorithm is to compare the symbols read by both heads. If they match, the tape advances to the left, on the leftmost head, and to the right on the rightmost head. When the tape can no longer move (the heads are spaced as adjacent records), the string is a palindrome. It is otherwise rejected.
This automaton is finite, in the sense that the heads and the machine have the same number of states regardless of the length of the tape. The interaction with the tape, reading and moving/manipulating, is mechanically as finite as the old finite control model.
The finite state diagram for this machine is simple. Here we use a two-symbol alphabet consisting of 'a' and 'b'.
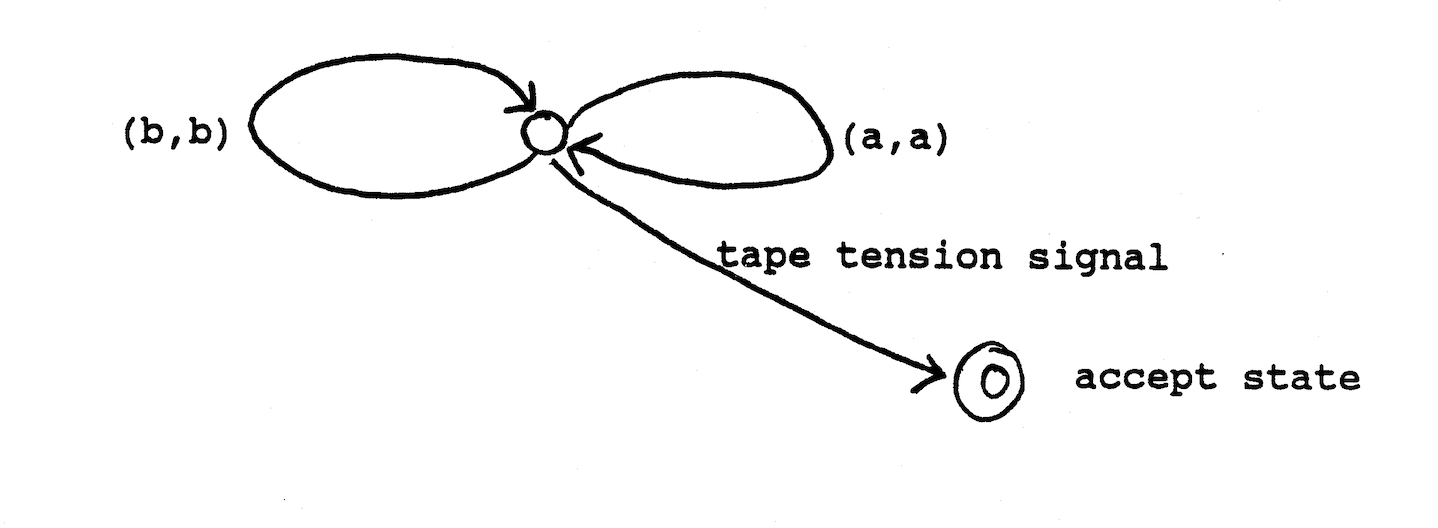
The ordered pairs represent the symbols read at any step by the left and right heads.
This palindrome, whose context-free grammar production is S-> aSa | bSb | {empty}, cannot be defined using FA regular expressions. If you accept that the machine is indeed finite, then there is no bijection between finitie automata and regular sets. This is of course a matter of definition, dealt with further in section V.
II. FA that accepts some non-CFL languages
These Multi-head finite auomata (MFA) can also accept languages that are not context-free. For example:
a^nb^nc^n
where n is a natural number.
The algorithm requires a three-head FA. With the initial configuration like so:
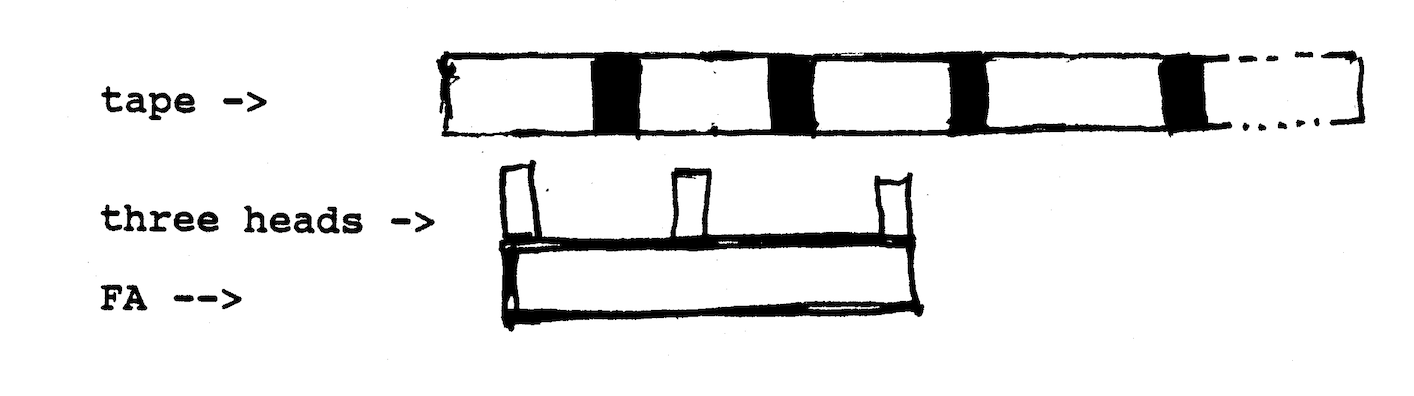
The MFA then needs to advance the tape over the rightmost head until it reaches a 'c', and the tape of the center head until it reaches a 'b'. From there it is sufficient to use the machine defined below (where 'rm' is the right end-marker of the tape, and with the tape always moving to the right over each head).
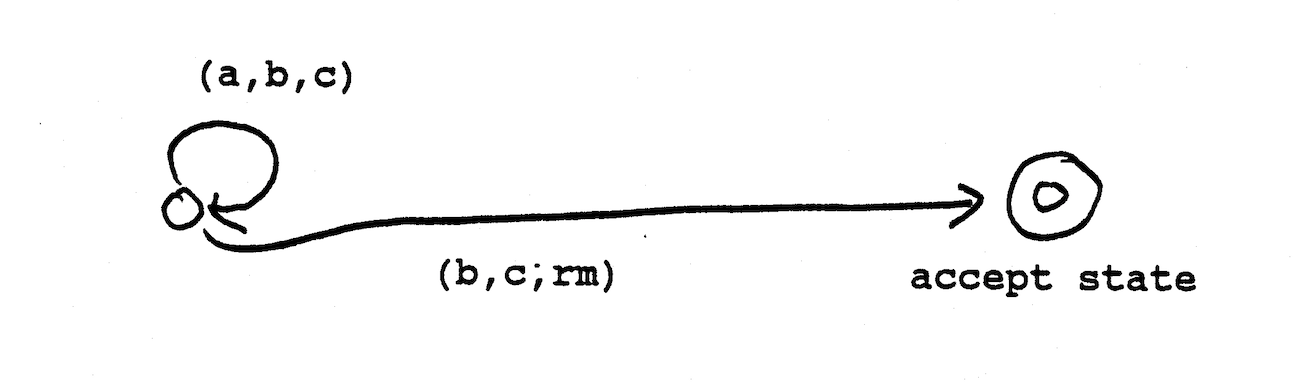
III. Machine and class notation
One might think that the notation of regular expressions with superscript extensions like the variables above, R for palindromes or mirror case, and perhaps a substitution notation for strings like "abbabaab" would be sufficient to express all languages acceptable to an MFA. However one further example will show these extensions to be insufficient and/or inappropriate. A notation representing the machine behavior turns out to be a direct way of describing a given language.
The task is to accept strings with a prime number of 1's. This too can be accomplished with a finite automaton.
The algorithm uses three read heads (or pointers). The first pointer increments through possible divisors, 2 through n-1 (though the program has no representation of n in it, being a finite state machine) [foreshadowing there]. Subsequent to each increment the third pointer counts to the divisor and resets iterativelywhile paralleld by the second pointer stepping through the entire string. Remainderless division sends the machine into a reject state; otherwise, after all the divisors are stepped through, the machine accepts the tape.
The notation below contains a few bits of shorthand to reduce the number of states to those pivotal to the algorithm. Eliminating these conveniences one has a language that provides a bijection to the set of possible MFA and a mapping to the languages accepted by them.
Standard notations
[ , , ] -- action triplet directing tape to move over three heads
+ or - -- move tape to left or right
( , , ) -- values over read heads; conditioon for state transition function
lm or rm -- left or right end-marker.
. -- any value
l -- lone member of our alphabet
(condition) -> state -- transition function
Shorthand
lm within [ , , ] -- move tape to the left endmarker (treated as a position
and in this shorthand as though many heads could be there at one time)
lm+1 -- move tape to the first symbol
(pl=p3) -- condition when heads 1 and 3 are in the same virtual position (?)
rm-1 within ( , , ) -- when head i on rightmost symbol
Note: multiple conditions are tested in order listed
1. initial state
[lm + 1, lm, lm}
(.,.,.) -> 2
2. increment divisor
[+, lm, lm]
(rm - 1, ., .) -> 3
(1, .,.) -> 4
3. accept state
4. dividing loop, first increment for third head
[,+,+]
(.,rm,.) -> 7
(pl = p3) -> 6
(.,1,1) -> 5
5. dividing loop, subsequent increments
[,+,+]
(.,rm,.) -> 7
(pl = p3) -> 6
(.,1,1) -> 5
6. reset dividing counter
[ , ,lm]
(.,.,.) -> 4
7. reject state
MFA are capable of quite varied behavior. One wonders what languages a Multi-head Pushdown Automata (MPDA) might accept with one and many stacks and finite control. More generally we need to ask what the characteristics of finite and infinite tasks [or behavior?] really are.
IV. MFA not LBA
Despite the power of these machines, there are context-free languages that none of them are able to accept. Since context sensitive languages (CSL) include CFL, and linear bounded automata (LBA) have been shown equivalent to CSL, this would imply that MFA are not LBA. I claim that this makes MFA finite.
To demonstrate that the context-free grammar
S -> aSSa | bSSb | c
canot be accepted by a finite number of states and heads, consider the form of such strings.
cc
a ac cc
b bc ca a cc cc
b ba a a aa a
b bc cb b
a aa a
b
b
Except for the single case of string 'c', every string generated by this grammar has the substring 'cc', occuring one or more times.
To accept a string in S one must first accept some substring, say q. Unless q is 'cc'. one must match it with its counterpart q' elsewhere in the string. The distance between these parts is arbitrary, so a finite state machine needs two heads to match them.
However, whichever 'direction' one matches and assimilates, either towards or away from a 'cc' (the centerpoint for the matching, otherwise another pair of heads will be necessary elsewhere in the string), one may run into a new 'peak' (i.e. another application of the aSSa or bSSb productions) an arbitrary length string that must be accepted before one can match further.
..... .. ..
cc b bc a aa a
b bc ca a cb b
ca a b ba a
a aa a
b bc
a a
Again, two heads are needed to accept this substring, but the current two are not available, since without them the finite state machine can have no idea what it has already matched, and will repeat itself. This problem will occur an arbitrary number of times.
Similarly, if one begins at a 'cc' (beginning at all of them implies an arbitrary number of heads) and works to accept the surrounding string, the same difficulty arises. This demonstrates by cases how no MFA can recognize an arbitrary string of S.
A class of automata that does not accept some CFL is certainly not equivalent to LBA, which could accept this tape by writing markers in the appropriate places. The Multi-head Finite Automata Languages (MFAL) therefore don't fit into the RS, CFL and CSL hierarchy, as shown below.
V. But is it finite?
Certainly MFA would be considered finite automata if we chose to call them such.
For example, the finite control model is not finite in some ver yimportant ways. Any arbitrary length tape can be placed on its single read head, making the number of possible states it can enter, including the tape as part of the machine, infinite. And the number of states, again included in the tape, given any particular tape is multiplied by the number of possible positions on that tape.
Also, the behavior of the single-head model is 'infinite' over time ... a 2-way finite automata can keep on reading indefinitely. And the combinationsof all the states an FA goes through over time are as limitless as the number of tapes it can read.
Yet we've agreed to call them finite. The do not fit our criteria for calling an automaton infinite.
Similarly an LBA's behavious of marking its tape and then interpreting it is not acceptable behavior for a finite machine, although it is certainly finite in many ways.
The MFA is an odd case. Being built like a single-head finite control is a strong case for its being considered finite, as is its limited ability. As a generalization of a finite automaton with many senses interacting with its environment, it's a very appealing model of a deterministic system in the real world.
[I leave the following 2002 observations here, even though they don't suffficiently incorporate the internalist/externalist distinction I descibed in the intro to this page. On first re-reading the 1987 essay after many years, I was curious about the external problem. Even though I sensed that it was entirely imaginary and mind-internal, like every logical contradiction, ever. So here's how a smart engineer can confuse themselves with their own imagined worlds when they don't consistently remain within the worldview of the natural sciences, and don't consistently ask themselves where the subject under investigation may actually exist.]
Notes, 2002.
The main point is that MFAs, machines with no internal variables, which would be considered to follow the finite control model, are more powerful than PDAs in some cases. Yet a PDA is considered an infinite machine, and an MFA is not. The point is that a PDA may have an infinite number of internal states, but an MFA externalizes states -- because taken as a whole, the tape adds significantly to the number of states available to the MFA.
But we don't usually take machines as a whole. We tend to isolate the machine's behavior, and separate its internal states from its environment, creating a logically consistent fantasy space, and partitioning data sets accordingly.
This paper still goes to the heart of a number of problems ... where does the machine begin and end? If we consider the machine to be a center, with the tape a supporting center, and the environment the tape flops around in to be yet another, then there's no need for such strict divisions. The notion of a finite machine which takes input from the real world is a very strange one, and should be tossed, in favor of a more straightfoward description of the machines -- finite internal states, infinite tape, externalized memory via the shape of the tape, etc.
It's interesting how this is reminiscent of our difficulty in understanding the central behavior in quantum mechanical systems -- how does the photon in the two slit experiment know about the existence of the other slit? Clearly an MFA is capable of more than meets the eye -- including some Universal Turing Machine-only level functionality. But, it does this by plodding away through finite states. How does the addition of more heads give it an infinite storage of states? It actually uses the outside world to do work, without being aware of it.
The reason this is intriguing, is that in quantum mechanics we have a behavioral theory not a contact mechanical one. And this is certainly a contact mechanical model. Probably we simply do not understand the systems we choose to define.